水了一个寒假,快开学了QAQ
过度~~~
何为分治?
分治:
将一个大问题用类似于二分的手法将其分成一半进行递归求解。
洛谷题 :平面最近点对
以该题为例: 求二维平面内n个点中的最短距离
思路:
我们可以将该图以最中间的点的x值分为两个区域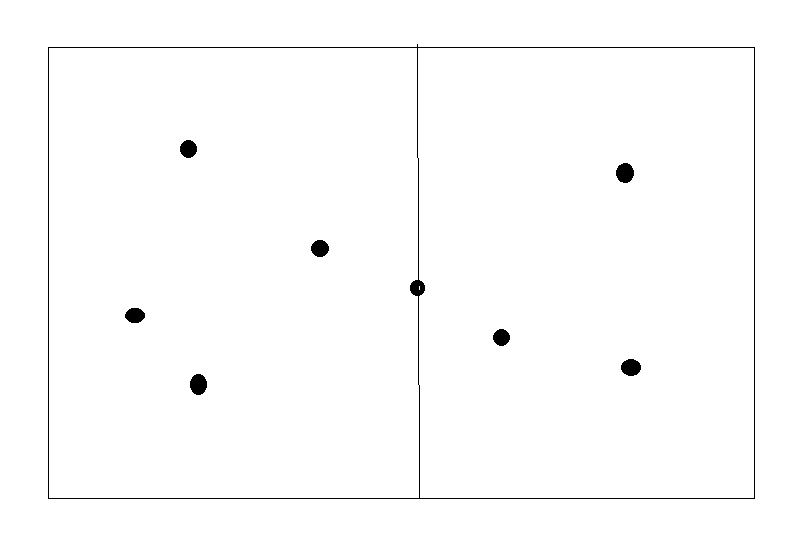
然后我们可以用分治的思想求最短距离d,其为两部分
1 : 求每个部分中最短距离 d
2 : 求跨越两个区域的最短距离 d
第一个部分我们很好理解,分治递归之。
第二个部分我们可以假设从已经从每个部分中得到一个最小距离d,我们假设中间点的坐标为 $x_1$,那么我们可以枚举 $x_1 - d < x <x_1 + d $ 的点查找是否有小于 $d$ 的值并更新。
因为对于以 $x_1$ 为中心,边长为 $d$ 的两个正方形, 显然枚举的点数一直在减小。
#include <bits/stdc++.h>
#define rep(i, n, m) for(int i = n; i <= m; ++i)
#define per(i, n, m) for(int i = n; i >= m; --i)
using namespace std;
const int N = 2e5 + 10;
pair<double, double> p[N];
double cal(pair<double, double> a, pair<double, double> b){
return sqrt((a.first - b.first) * (a.first - b.first) + (a.second - b.second) * (a.second - b.second));
}
double get(int l, int r){
if(l == r) return INF;
if(l + 1 == r) return cal(p[l], p[r]);
int mid = l + r >> 1;
double x = p[mid].first;
double d = min(get(l, mid), get(mid + 1, r));
for(int i = mid; i >= l && x - p[i].first < d; -- i){
for(int j = mid + 1; j <= r && p[j].first - x < d; ++ j){
double res = cal(p[i], p[j]);
d = min(res, d);
}
}
return d;
}
int main()
{
//ios::sync_with_stdio(0); cin.tie(0);
int n; cin >> n;
rep(i, 1, n){
cin >> p[i].first;
cin >> p[i].second;
}
sort(p + 1, p + 1 + n);
printf("%.4lf", get(1, n));
return 0;
}
然后回到正事
洛谷题:点分治
题意:给定一棵 n 个节点的数,m 次询问每次问是否存在距离为 k 的点对
思路:
对于一颗树,我们考虑选择一个根节点 $root$,那么删除该根节点后,就会出现若干棵子树
然后我们考虑的距离有两种: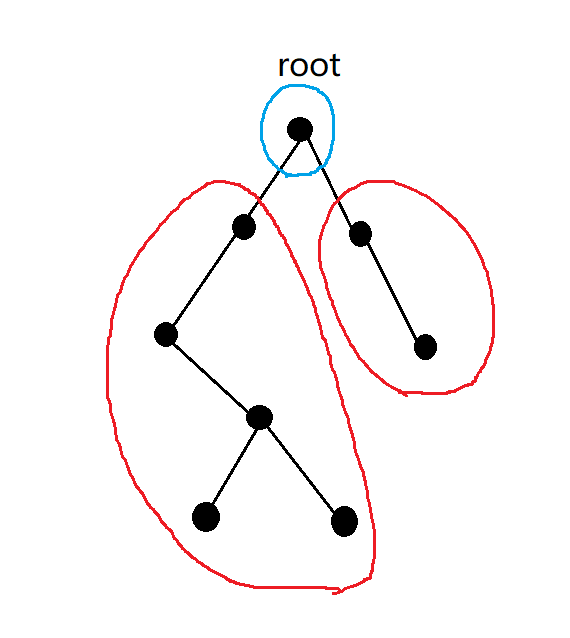
1 :一颗子树中的两个节点之间的距离
2 :两个属于不同子树的节点之间的距离,这个路径是经过根节点的。(如果有一个节点是根节点,那么可以看成第二种情况下一个节点到根节点的距离为 0)
如果我们枚举每一个节点为根节点,那每一个递归层的复杂度是 $O(nlogn)$,如果一颗树的路径是一条线性链表的话,那复杂度就变成了$O(n^2logn)$,直接寄了,所以我们可以考虑找到一棵树的重心作为根节点,那么我们的复杂度就可以变成$O(nlog^2n)$
(树的重心:它的子树的数量最大值最小)
我们可以用一个递归来找重心
void get_root(int u, int pre, int sum){
siz[u] = 1; mx[u] = 0;
for(int i = head[u]; i; i = ne[i]){
int to = e[i];
if(to == pre || vis[to]) continue; //如果当前点已经做过重心
get_root(to, u, sum);
siz[u] += siz[to]; //子树大小相加
mx[u] = max(mx[u], siz[to]); //找最大子树大小
}
mx[u] = max(mx[u], sum - siz[u]); //当前子树外的所有点 sum - siz[u]
if(mx[u] < mx[root] || !root) root = u; //如果最大子树大小比 mx[root]小就更新
}
另外,在一个根节点下面的所有dist都知道了以后,如果两个点是同一颗子树中的,那他俩的dist相加肯定不是正确的路径长度,所以我们可以用一个col来标记当前节点属于哪一棵子树,最后我们二分该根节点下的所有节点,如果不属于同一颗子树且满足dist[l] + dist[r] == query[i] ,则答案存在
sort(q + 1, q + 1 + tol, cmp); //我们对所有点按 到 根节点的距离长度排序
rep(i, 1, m){
int l = 1, r = tol;
if(ok[i]) continue;
while(l < r){
int x = q[l], y = q[r];
if(dist[x] + dist[y] < query[i]){
l ++;
}else if(dist[x] + dist[y] > query[i]){
r --;
}else if(col[x] == col[y]){
if(col[y] == col[q[r - 1]]) r --;
else l ++;
}else {
ok[i] = 1;
break;
}
}
}
最终代码
#include <bits/stdc++.h>
#define rep(i, n, m) for(int i = n; i <= m; ++i)
#define per(i, n, m) for(int i = n; i >= m; --i)
using namespace std;
const int N = 2e5 + 10;
int ne[N], w[N], e[N], head[N], cnt = 0; //邻接表
int n, m, root, ok[N], query[N], siz[N], mx[N], vis[N];
int tol, q[N], dist[N], col[N];
/*
ok:是否存在点对满足解 query:每次询问的k值 siz:以当前为根节点的子树大小
mx:以当前节点为根节点,其子树中大小的最小值 vis:当前节点是否当过重心
tol:队列的大小, q:队列
dist:当前节点到根节点的距离 col:当前点属于哪棵子树
*/
void add(int a, int b, int c){
e[++cnt] = b, w[cnt] = c, ne[cnt] = head[a], head[a] = cnt;
}
bool cmp(int a, int b){
return dist[a] < dist[b];
}
void get_root(int u, int pre, int sum){
siz[u] = 1; mx[u] = 0;
for(int i = head[u]; i; i = ne[i]){
int to = e[i];
if(to == pre || vis[to]) continue;
get_root(to, u, sum);
siz[u] += siz[to];
mx[u] = max(mx[u], siz[to]);
}
mx[u] = max(mx[u], sum - siz[u]);
if(mx[u] < mx[root] || !root) root = u;
}
void get_dist(int u, int pre, int dis, int camp){
q[++tol] = u; // 入队列
dist[u] = dis;
col[u] = camp; // u节点属于子树 camp
for(int i = head[u]; i; i = ne[i]){
int to = e[i];
if(to == pre || vis[to]) continue;
get_dist(to, u, w[i] + dis, camp);
}
}
void cal(int u){
tol = 0;
q[++ tol] = u;
dist[u] = 0;
col[u] = u;
for(int i = head[u]; i ; i = ne[i]){
int to = e[i];
if(!vis[to]) get_dist(to, u, w[i], to);
}
sort(q + 1, q + 1 + tol, cmp);
rep(i, 1, m){
int l = 1, r = tol;
if(ok[i]) continue;
while(l < r){
int x = q[l], y = q[r];
if(dist[x] + dist[y] < query[i]){
l ++;
}else if(dist[x] + dist[y] > query[i]){
r --;
}else if(col[x] == col[y]){
if(col[y] == col[q[r - 1]]) r --;
else l ++;
}else {
ok[i] = 1;
break;
}
}
}
}
void solve(int u){ // 分治
vis[u] = 1;
cal(u);
for(int i = head[u]; i; i = ne[i]){
int to = e[i];
if(!vis[to]){
root = 0;
get_root(to, 0, siz[to]);
solve(root);
}
}
}
int main()
{
//ios::sync_with_stdio(0); cin.tie(0);
cin >> n >> m;
rep(i, 1, n - 1){
int u, v, w; cin >> u >> v >> w;
add(u, v, w); add(v, u, w);
}
rep(i, 1, m){
cin >> query[i];
}
mx[0] = n;
get_root(1, 0, n);
solve(root);
rep(i, 1, m){
if(ok[i]) cout << "AYE" << '\n';
else cout << "NAY" << '\n';
}
return 0;
}
/*
4 4
1 2 3
2 3 2
3 4 1
2
3
1
4
*/
