欧几里得延申

2023/1/14 数论裴蜀定理扩展欧几

md鼻塞真难受

欧几里得辗转相除法：求a，b的最大公约数

int gcd(int a, int b){
  return a % b == 0 ? b : gcd(b, a % b);
}

几何证明：

问可以用最大边长为多少的正方形填满这个 20 * 56 的长方形 ?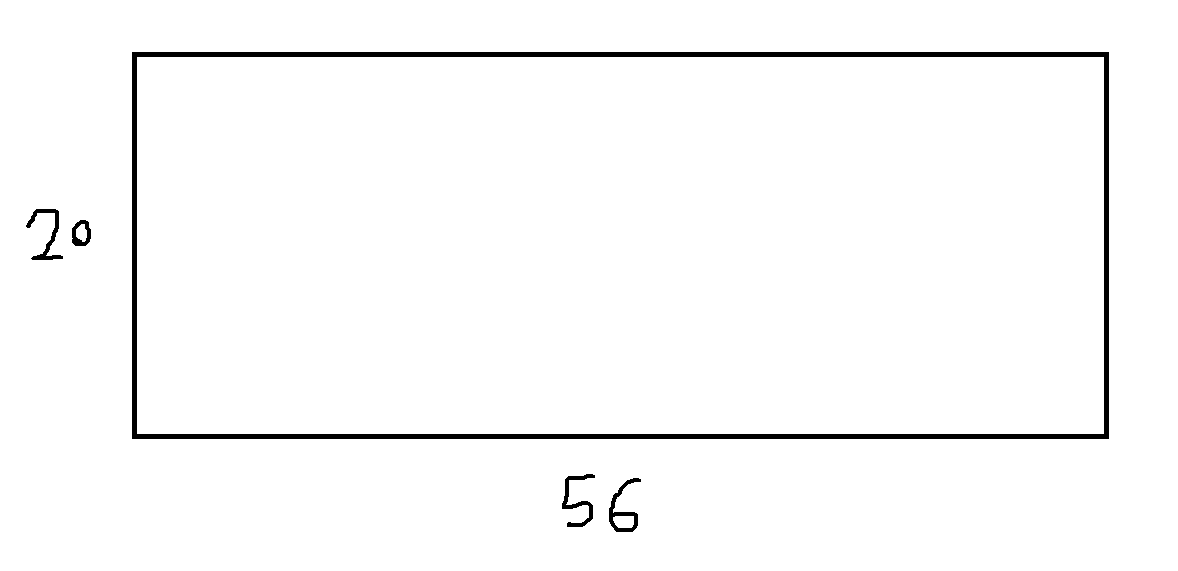

我们首先必然可以使用20边长的去填，于是得到了余下的16*20的长方形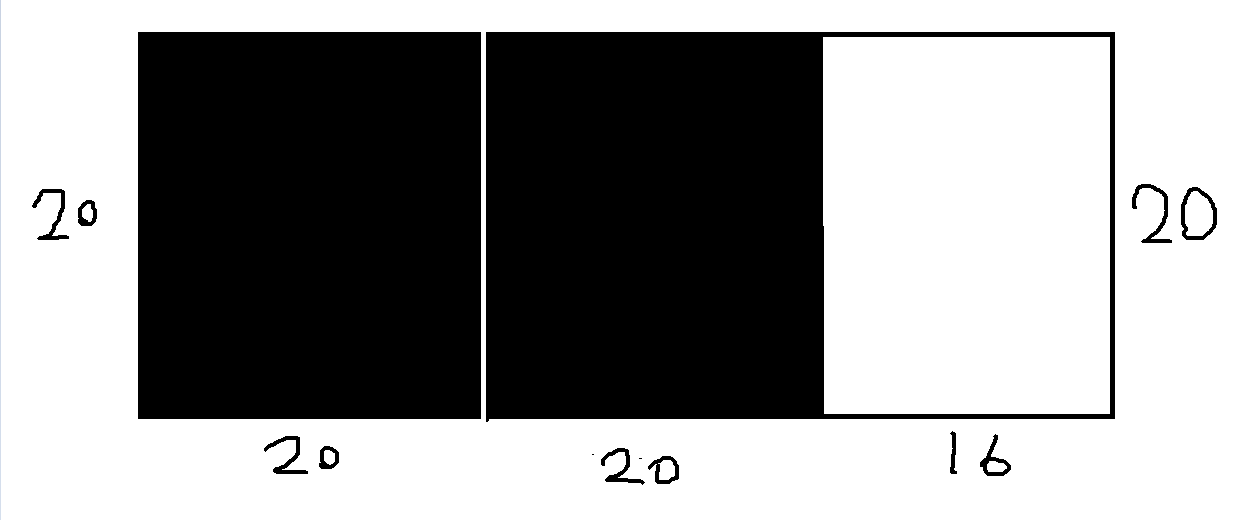

以此类推，我们可以得到这样子的填补，显而4是最大的正方形可以填补该最大长方形，所以4就是20和56的最大公约数。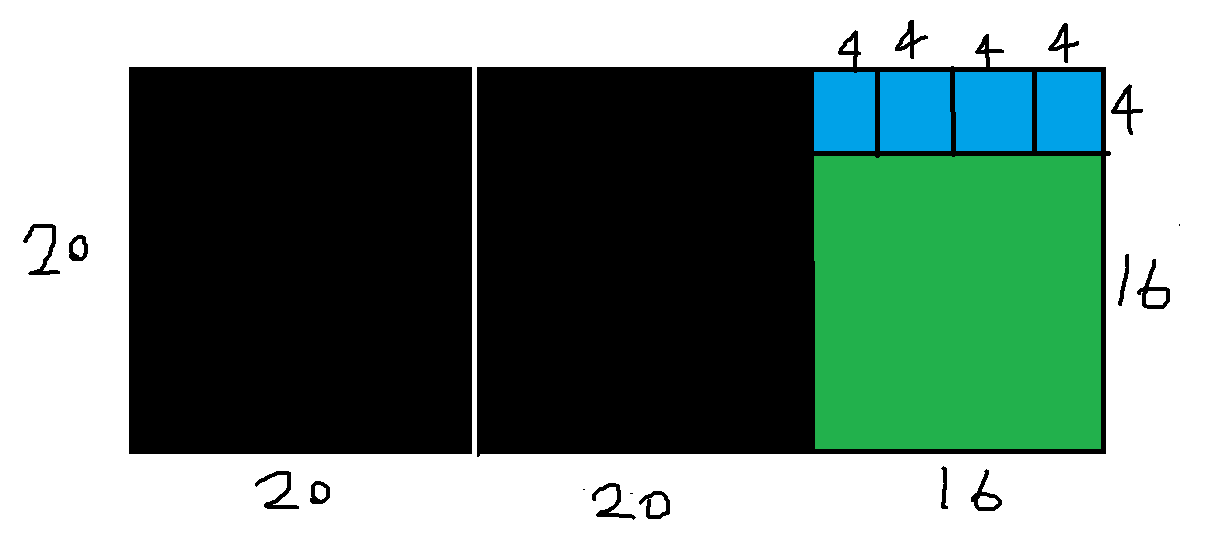

：

 56 ÷ 20 = 2 ······ 16
 20 ÷ 16 = 1 ······ 4
 16 ÷  4 = 0

我们设余数是 $r$，被除数是 $a$，除数是 $b$，商是 $c$，$a、b$的最大公约数是 $s$，得 $r = a - b*c$
又因为 $s|r, s|b$
$gcd(56,20) =gcd(20,16)=gcd(16,4)=4$
则
$gcd(a,b) = gcd(b, a$%$b) $

裴蜀定理: （我写的是狗屎，）

设 $a,b$ 是不全为零的整数，则存在整数 $x,y$, 使得 $ax+by=gcd(a,b)$

我们可以简单发现，如果 $ax+by=d$, 则 d 一定为 $gcd(a,b)$ 的倍数，

由 $ax+by=$ $a_1 r x+$ $b_1ry=d$，显得 $d$ 也是 $r$ 的倍数

同时我们可得若当 $ax+by=1$ 有解，则 $a，b$ 互质。

扩展欧几里得求解

给定两个整数 $a、b$,求得一组解 $x、y$ 使得 $ax+by=d$
当 $b=0$ 时 $ax+by=a$ 故而 $x=1,y=0$

当 $b≠0$ 时
$gcd(a,b)=gcd(b,a$%$b)$ 且 $bx′+(a$%$b)y′=gcd(b,a$%$b)$

$bx′+(a−⌊a/b⌋×b)y′=gcd(b,a$%$b)

$ay’+b(x’−⌊a/b⌋×y’)=gcd(b,a$%$b)=gcd(a,b)$

得 $x=y’,y=x’−⌊a/b⌋×y’$

然后我们可以采用递归求解

void ex_gcd(int a, int b, int &x, int &y){
    if(b == 0){
        x = 1, y = 0;
        return ;
    }
    ex_gcd(b, a % b, y, x);
    y = y - a / b * x;
}
void solve()
{
    int a, b, x, y; cin >> a >> b;
    ex_gcd(a, b, x, y);
    cout << x << ' ' << y << '\n';
}

中国剩余定理：

给定 $a$ 数组和 $n$ 数组(其中 $n_1$, $n_2$,…, $n_k$两两互质)，可用该定理求解如下方程组

其主要有三步：

1、计算每一个$n_i$的乘积$M$，同时计算

2、然后对于每一个 $m_i$ 求 $m_i$ $c_i$ $=1(mod$ $n_i$)，也就是$m_i$在$n_i$上的逆元，以为每个$n_i$都是互质的，所以该逆元一定存在。
最后

3、求得

简单证明

我们易知，且

这意味着所有 $a_im_it_i$ 的和在模 $M$ 的情况下满足以上所有方程组。

LOADING